Induljunk el a kályhától 1. – A hőtan története

Az “Induljunk el a kályhától” cikksorozat a MACSOI kályhás szakújságban jelent meg az évek során folyamatosan.
Ezekben a cikkekben a hőtannal, a termodinamikával foglalkozunk, hőfolyamatokkal összefüggő legáltalánosabb törvényszerűségeket és ezek fizikai alapjait – hőmérséklet, hő, energia, hőátadás fogalmát – ismertetjük.

Jóllehet e témák feldolgozása során több kötetnyi szakirodalmat lehetne közzétenni, nyilvánvaló, hogy sorozatunkban – terjedelmi korlátok miatt – csak az alapfogalmak kifejtésére szorítkozunk. Fontos célunk azonban, hogy a törvényszerűségek leírását és magyarázatát gyakorlati kontextusba helyezzük.

A hőtan története, történeti áttekintése

A történelmi áttekintést azért tartjuk szükségesnek, mert – a hőismeretek fontosságára való tekintettel – segíti kiküszöbölni a fogalmi pontatlanságokat, amelyek a mai napig beleívódtak a mindennapi szóhasználatba, holott a korszerű fizikai ismereteknek némileg ellentmondanak. A hőtan akkor vált a fizika részévé, amikor a hőmérsékletet mérni tudták. Az első hőmérők az 1500-as évek végén, Galilei korában készültek el; a tudós maga is tökéletesítette működésüket. Később különböző hőmérsékleti skálát állítottak fel a fizikusok: Fahrenheit 1724-ben, Reaumur 1730-ban és Celsius 1742-ben. E mérési módok a világ különböző tájain terjedtek el. Ugyanakkor a hőmérséklet megbízható mérése lehetővé tette a kalorimetria kialakulását.

1. Joseph Black caloricum (hőfolyadék) elmélete

A hőtan történetében a hőmérséklet és a hőmennyiség között először Joseph Black tett különbséget 1760 körül. (Érdekességként említhetjük meg, hogy Black legkiválóbb tanítványa James Watt, a gőzgép tökéletesítője volt). Black munkásságának köszönhetjük a hőtan olyan alapvető fogalmainak megjelenését, mint a hőmennyiség, a fajhő, a latens (rejtett) hő, az olvadáshő, a párolgási hő. Black úgy vélte, hogy a hő valami folyadék, fluidum, szubsztancia, amelyet minden test tartalmaz. Ezt a hőfolyadékot „caloricum”-nak nevezte el. Ugyanakkor Black – vérbeli kísérleti fizikusként – tisztán látta, hogy a calorikumelmélet csupán hipotézis, mert hőfolyadékot önállóan senki sem tudott megfigyelni. Viszont a tudós meghatározta a caloricum (mai szóhasználattal élve a hőmennyiség) mértékegységét, a kalóriát. Ezek szerint 1 kalória (1 cal) hőmennyiség szükséges ahhoz, hogy 1 gramm víz hőmérsékletét 1 °C-kal megnöveljük.

A caloricumelmélet következtében terjedtek el az olyan ma is használatos kifejezések, mint a hőátadás, a hőfelvétel, a hőleadás, a hőközlés, a hőfelszabadulás, amit akkoriban úgy értettek, hogy valódi szubsztancia, vagyis hőfolyadék átadásáról, felvételéről, felszabadulásáról, stb. van szó. Annak ellenére, hogy ma már világosan látjuk, hogy hőfolyadék (caloricum) nem létezik, kalorimetriai problémák esetén ma is jól tudjuk használni a régi tárgyalásmódot. Gondoljunk csak az ilyen megfogalmazásra: „a melegebb test által leadott hő megegyezik a hidegebb test által felvett hőmennyiséggel”. E leírásmódot nyugodtan használhatjuk, de közben ne felejtsük el, hogy a hőközlés mindig energiaátadást jelent.

1.2 Benjamin Thompson – Rumford gróf: A hő mozgás

Az eddigiekben a caloricumelmélet sikereiről szóltunk, a továbbiakban azonban a cáfolatával foglalkozunk. A gyakorlat ugyanis az elmélet elé szaladt, mert anélkül, hogy a hőmennyiség természetét ismerték volna, megvalósították a hőenergia ipari használatát, megalkották a gőzgépet. Ez már sugallta azt is, hogy valamilyen kapcsolat van a hő és a munka között. A hőfolyadék-elmélettel azonban nem tudták megmagyarázni a súrlódáskor keletkező hőt. A hőtan történetében megjelent egy új elmélet, amelyet Benjamin Thompson, vagy más néven Rumford gróf (1753-1814) képviselt, miszerint „a hő mozgás”.

Rumford részletesen megvizsgálta az ágyúcsövek kifúrásakor fellépő hőviszonyokat és megállapította, hogy állandó dörzsöléssel egy anyagdarabból tetszőlegesen sok hőt tudunk kivenni, ha elegendően hosszú ideig dörzsöljük, vagyis a hő nem lehet anyagi szubsztancia. Rumford gróf egy ideig a bajor katonai arzenál vezetője volt, így érthető, miért az ágyúcsövek kifúrásakor fellépő súrlódást vizsgálta.

Rumford nagyon közel járt a mechanikai és hőenergia azonosságának felismeréséhez, mérési eredményeiből utólag ki lehet olvasni a későbbiekben nagy szerepet játszó ekvivalencia (egyenértékűség) számértékét is.

1.3 James Prescott Joule – a hő mechanikai egyenértékének meghatározása

Az akkori szóhasználat szerint „a hő mechanikai egyenértékét” a hőtan törtnetében végül is James Prescott Joule határozta meg, eredményét 1845-ben publikálta. A francia eredetű családból származó Joule már Angliában született, Manchesterben élt, s magát angolnak tekintette. Nevét szokás francia kiejtéssel „zsúl”-nak mondani, de helyes az angolos „dzsaul” kiejtés is. Személyében az egyik utolsó autodidakta tevékenykedett, aki érdemben hozzájárult a fizika fejlődéséhez.

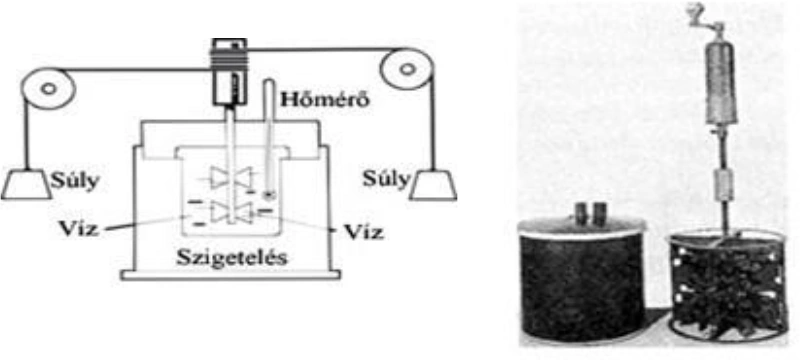
Súlyok segítségével lapátokkal ellátott kereket hajtott meg, amely egy vízzel telt edényben forgott. A víz közegellenállása miatt a lapátkerékre nagy súrlodásos típusú fékezőerő hatott, aminek következtében a kerék forgása és a súlyok mozgása is hamar egyenletessé vált. A súlyok helyzeti energiájának változása végül is a víz termikus energiáját növelte, amit a tudós hőmérő segítségével nyomon tudott követni. Természetesen Joule a mechanikai munkát nem joule egységekben mérte, hiszen ezt csak sokkal később nevezték el róla, s a kalóriát sem a mai értelemben használta. Eredeti megállapítása így hangzott: „1 font víz hőmérsékletét 1 Fahrenheit-fokkal 772 láb-font munkával tudjuk megnövelni.” Joul mérései óta tudjuk tehát, hogy 1 kalória 4,186 joule munkának vagy energiának felel meg, mely értéket legtöbbször 4,2 J értékre kerekíthetünk.